Normalizing Flow 설명 – 정의, 특징, 딥러닝 모델들

요약

Normalizing Flow의 정의와 특징을 알아봅니다. 딥러닝으로 Normalizing Flow를 구현하기 위한 조건을 살펴봅니다. 마지막으로 딥러닝으로 Normalizing Flow를 구현한 모델인 NICE, RealNVP, Glow를 살펴봅니다.

1. 들어가며

이번 글에서는 Normalizing Flow에 대해 설명합니다. 먼저 Normalizing Flow의 정의를 살펴보고요, 수식을 따라가며 특징을 살펴보겠습니다. 마지막으로 딥러닝으로 구현한 Normalizing Flow 모델들을 살펴봅니다.

2. Normalizing Flow 정의

먼저 Normalizing Flow의 정의를 알아보겠습니다. Normalizing Flow는 생성 모델 (Generative Model) 중 하나입니다. 대표적인 생성 모델로는 GAN, VAE 등이 있죠. 생성 모델이란 데이터 (보통 이미지)를 생성하는 모델을 의미하는데요. 동작 과정을 간단하게 표현하면 다음과 같습니다.

고차원 데이터 x를 저차원 데이터 z로 mapping 해주는 함수 f가 있고요. 반대로 저차원 데이터 z를 고차원 데이터 x로 mapping해주는 함수 g가 있습니다. GAN, VAE, Normalizing Flow는 모두 생성 모델이고 위와 같은 동작 구성을 따릅니다. 다만 함수 f와 g를 구성하는 방법이 다르죠.

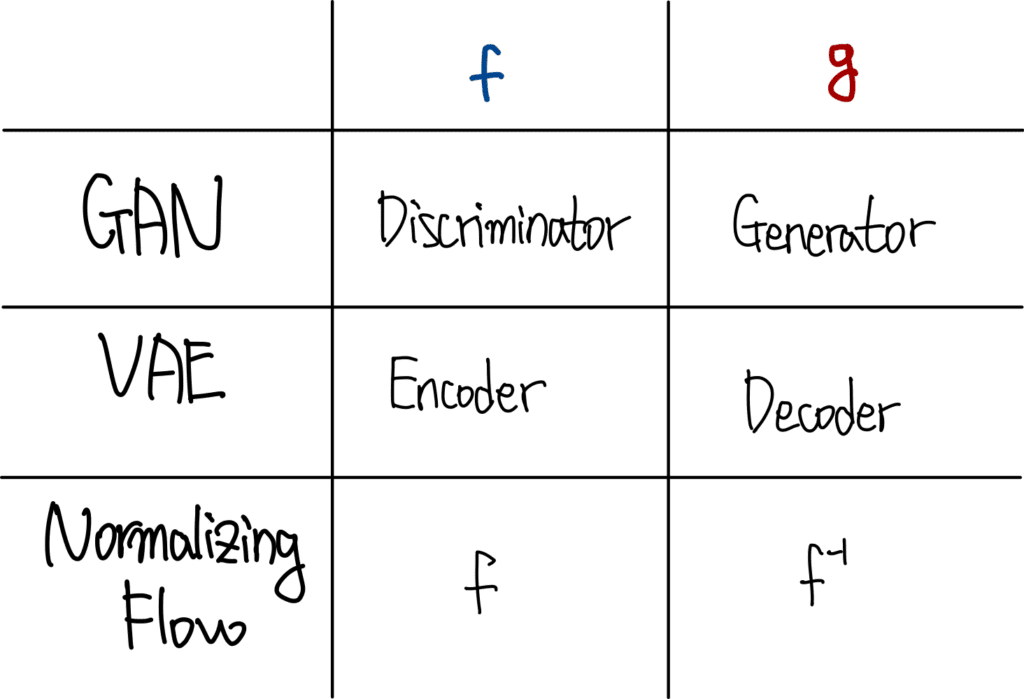
위 표는 GAN, VAE, Normalizing Flow에서의 함수 f와 g를 비교한 표입니다.
먼저 GAN을 보겠습니다. GAN은 위의 그림과 조금은 다르지만, 이미지를 생성해주는 g에 해당하는 Generator가 존재합니다. 그리고 이렇게 생성된 이미지의 진위 여부를 판단하는, 즉 f에 대응되는 Discriminator가 존재하죠.
반면 VAE에서는 f에 해당하는 역할을 하는 모듈을 Encoder라고 부릅니다. 반대로 g에 해당하는 역할을 하는 모듈을 Decoder라고 부르죠. Encoder와 Decoder는 모두 CNN 등 딥러닝 모델을 사용하며 Backpropagation으로 학습합니다.

여기까지 알 수 있는 점은 GAN과 VAE에서의 f와 g는 별개의 함수라는 것입니다. GAN에서는 Generator와 Discriminator로 전혀 다른 함수였죠. VAE에서도 Encoder와 Decoder라는 전혀 다른 함수로 구성됩니다. 이 점이 Normalizing Flow와의 가장 큰 차이점인데요. Normalizing Flow에서는 g가 별개의 함수가 아닙니다. Normalizing Flow에서의 g는 f의 역함수로 구성됩니다. 그 말은 g를 통해 나오는 값은 x’이 아닌 x가 나온다는 말이죠.

3. Normalizing Flow의 특징

Normalizing Flow는 f와 f의 역함수로 구성된다는 점이 가장 큰 특징이라고 했는데요. 이로 인해 갖게 된 Normalizing Flow만의 특징이자 가장 강력한 장점이 있습니다.

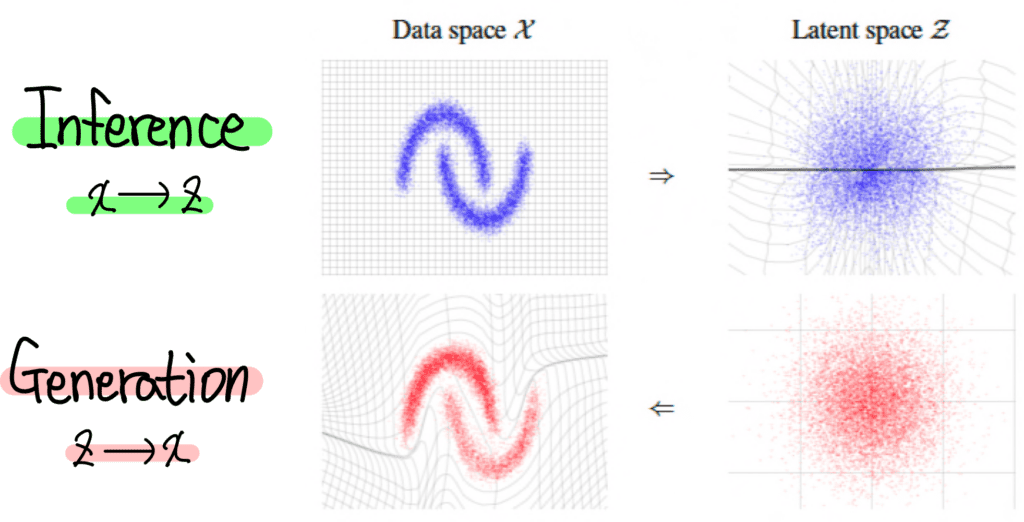
위 그림은 Normalizing Flow의 Inference 과정과 Generation 과정을 표현한 그림입니다. 고차원 데이터 X를 저차원 공간 Z로 Mapping 해주는 Inference 과정이 있고요. 반대로 저차원 공간 Z로부터 고차원 공간 X로 Mapping 해주는 Generation 과정이 있습니다.

이때 x와 z는 함수 f와 f의 역함수로 구성 되어있죠. 따라서 x의 확률 분포는 z의 확률 분포로 표현할 수 있습니다. 그 말은 z의 확률 분포를 알고 있다면 x의 확률 분포를 구할 수 있다는 말이죠. 또 다시 그 말은 이미지 등을 생성하는 완벽한 생성 모델이 될 수 있다는 말이고요.

이게 어떻게 가능한지 수식을 따라가며 생각해보겠습니다.

먼저 x와 z는 함수 f와 f의 역함수로 연결되어 있습니다. 이는 수식으로 이렇게 표현할 수 있죠.

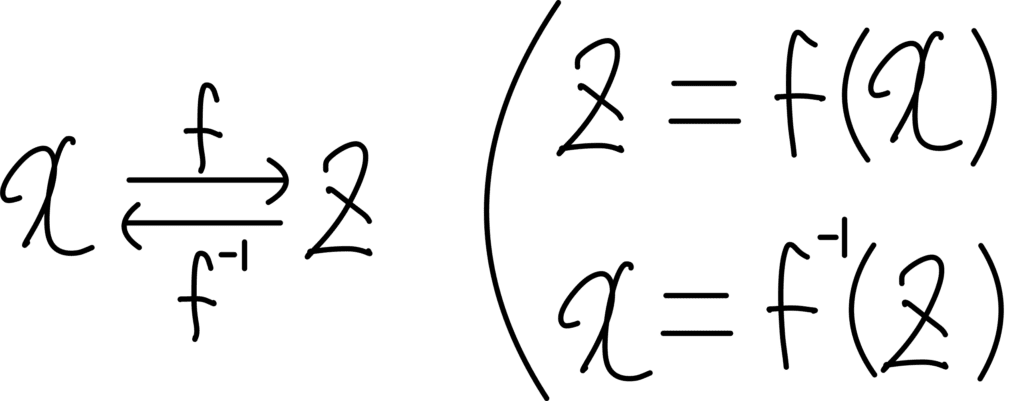
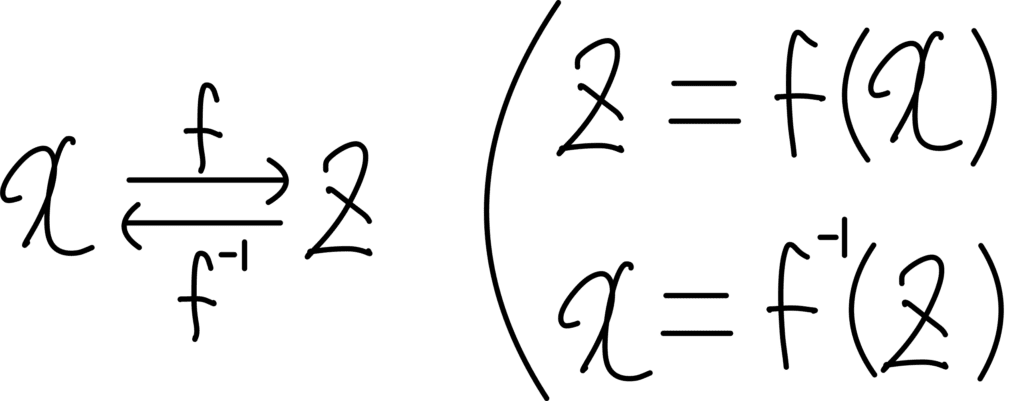
x와 z의 확률 분포 합은 1이 되어야 합니다. 이를 수식으로 표현하면 이렇습니다.

위 식을 각각 x에 대해 미분해주면 다음과 같은 식을 얻을 수 있습니다.

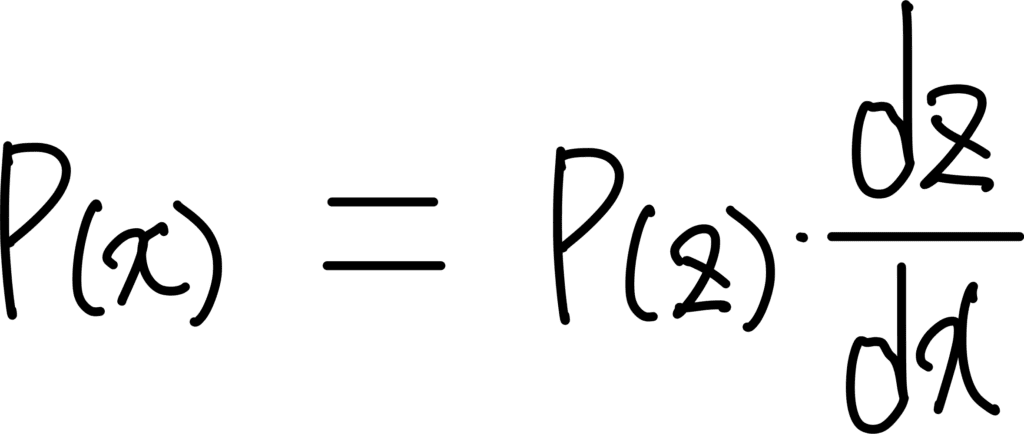
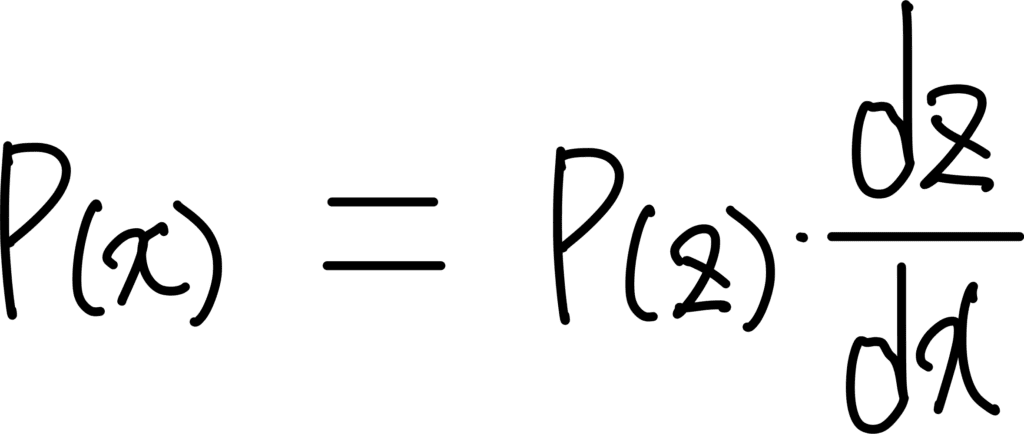
이를 행렬식으로 표현하면 다음과 같죠.

위 식을 우리에게 조금 더 익숙한 Log Likelihood로 표현해주기 위해 양변에 Log를 씌우면 다음과 같이 변형됩니다.

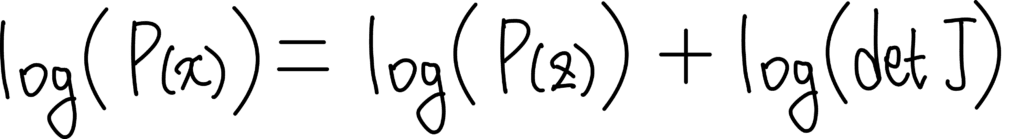
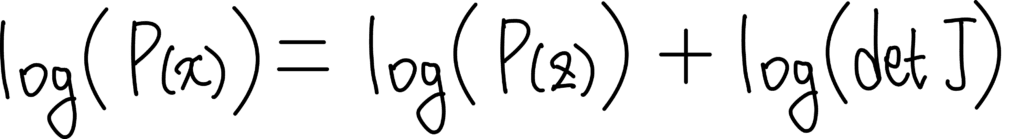
보통 x는 매우 복잡한 분포를 갖잖아요? 이미지처럼요. 따라서 x와 z는 하나의 함수로 연결하기는 어렵습니다. 많은 함수를 이어서 연결해주죠. 아래 그림 처럼요.

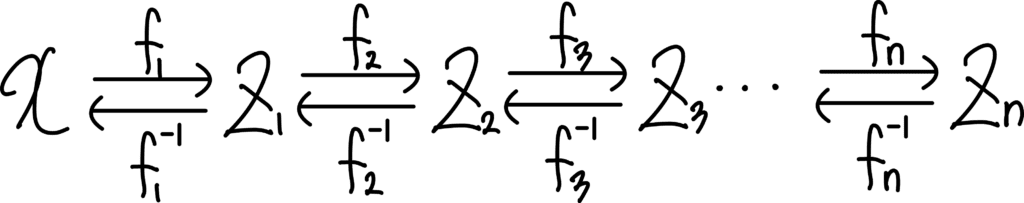
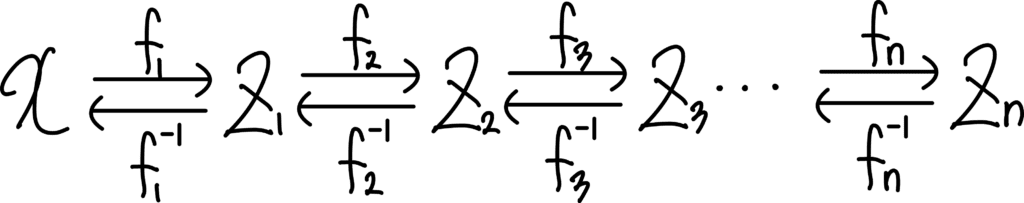
이런 상황에서는 위의 수식4번은 이렇게 변형될겁니다.

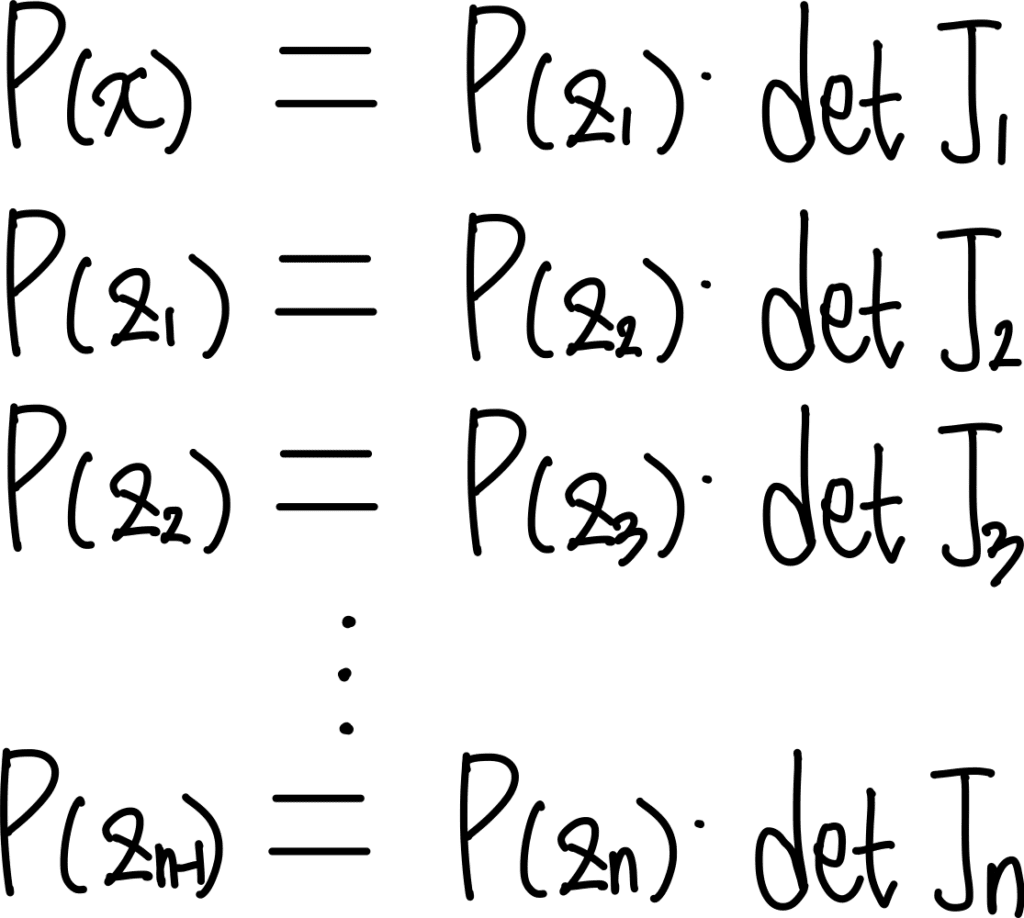
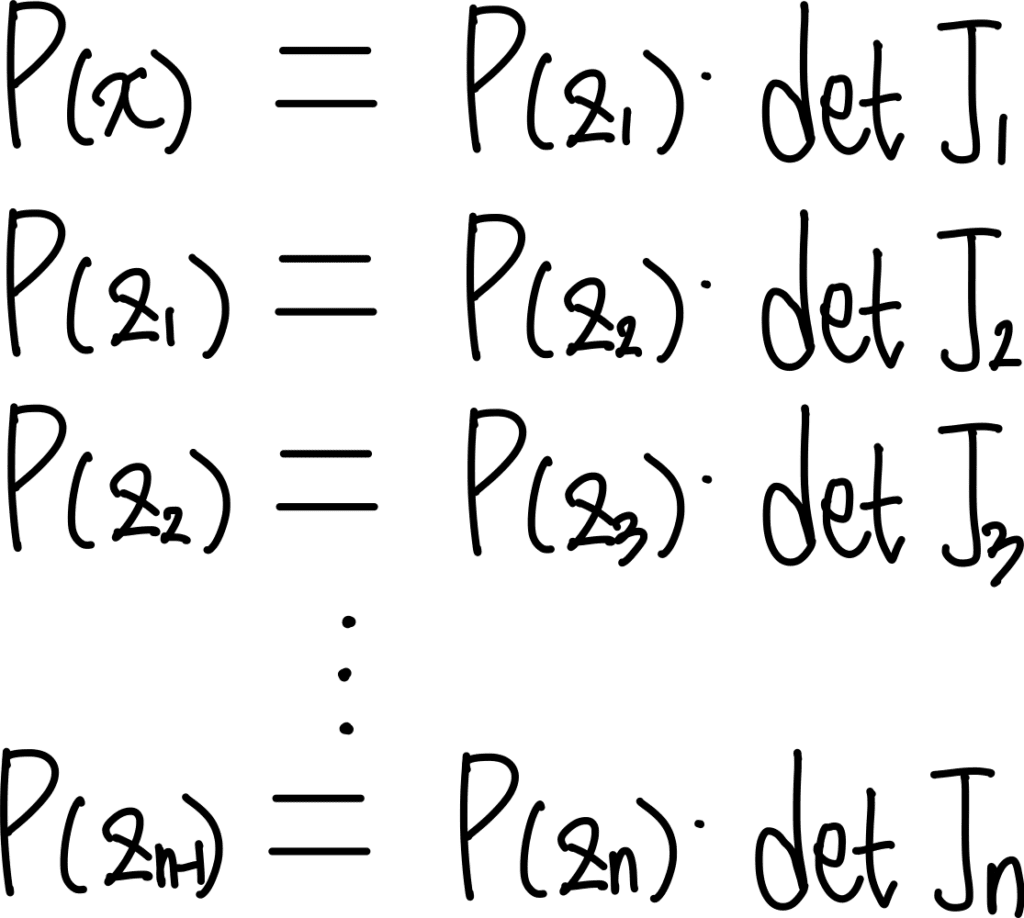
이를 하나로 합쳐주면 이렇게 표현해줄 수 있죠.

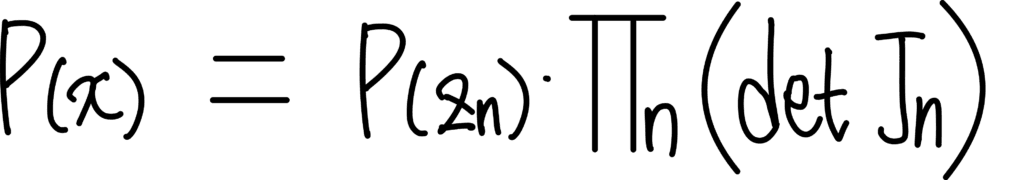
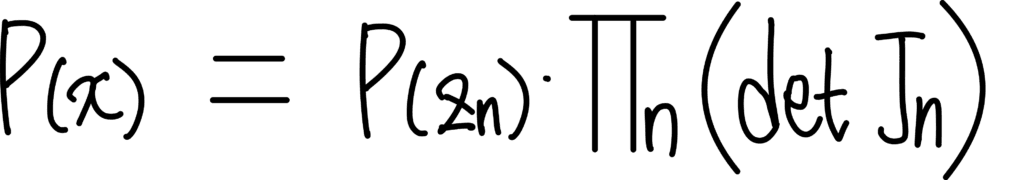
최종적으로 Log Likelihood는 이렇게 표현됩니다.

위의 수식을 보면 x의 확률 분포를 알기 위해서는 두 가지 조건이 충족되어야 합니다.
첫 번째는 z의 확률 분포를 계산할 수 있어야 합니다. 때문에 보통 Normalizing Flow에서는 z를 Gaussian Distribution을 사용합니다. Gaussian Distribution의 확률 분포는 수식으로 계산할 수 있으니까요.
두 번째는 Jacobian의 Determinant를 계산할 수 있어야(tractable) 합니다. 따라서 함수 f를 선택할때는 Jacobian의 Determinant를 쉽게 계산할 수 있는지 고려해야 하죠.

4. 딥러닝으로 구현한 Normalizing Flow 모델들

위에서 살펴본 것 처럼 Normalizing Flow는 수식으로 깔끔하게 설명되는 생성 모델입니다. 하지만 GAN, VAE와는 달리 딥러닝을 사용하여 구현하는건 쉽지 않았는데요. 이번 챕터에서는 딥러닝으로 Normalizing Flow를 구현하기 위한 조건과 이를 해결하고 구현한 대표적인 모델들을 살펴봅니다.

4-1. 딥러닝 구현을 위한 조건

딥러닝 모델을 사용하여 Normalizing Flow를 구현하기 위해서는 두 가지 조건이 필요합니다.

첫 번째 조건은 함수 f의 역함수가 존재해야 한다는 것입니다.

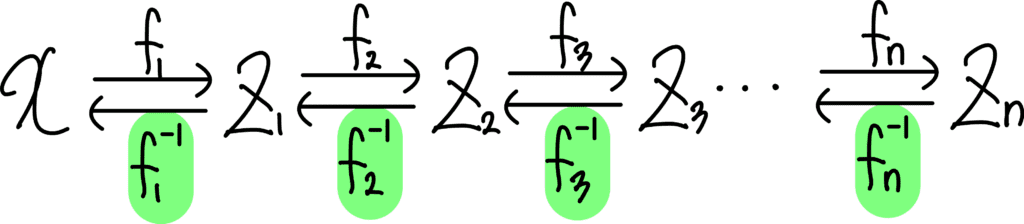
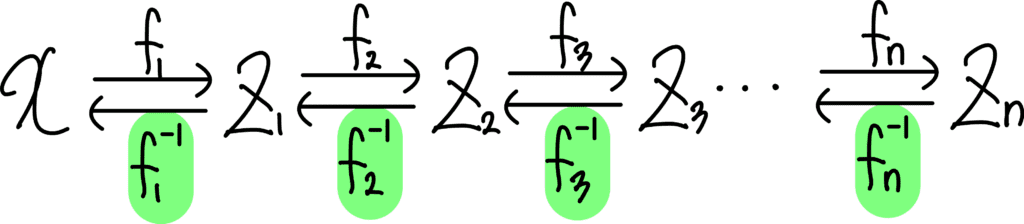
위 그림은 전에 보았던 x와 z가 함수 f와 f의 역함수들로 연결된 그림입니다. 이때 f가 역함수가 존재하지 않는 함수라면 위 그림 자체가 성립하지 않겠죠. 그런데 생각해보면 딥러닝에 사용되는 많은 함수들은 역함수가 존재하지 않습니다. 단순하게 떠올려봐도 Convolution, Pooling, ReLU 등은 역함수가 존재하지 않죠. y값에 대응되는 단 하나의 x를 찾을 수 있는지 생각해보면 간단하게 알 수 있습니다. 따라서 딥러닝으로 Normalizing Flow를 구현하기 위해서는 먼저 역함수가 존재하는 함수를 구현해야 합니다.

두 번째 조건은 Jacobian의 Determinant를 계산할 수 있어야 합니다.

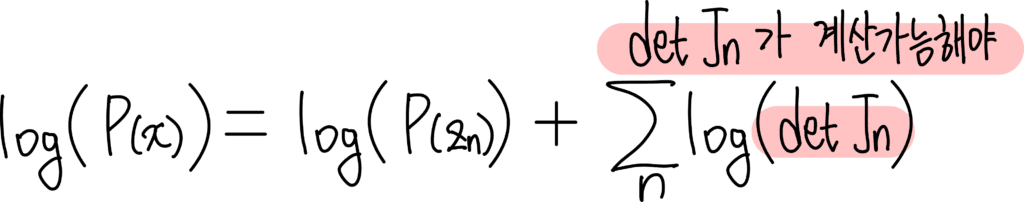
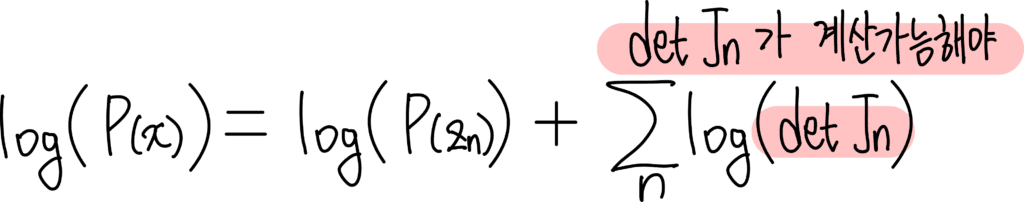
위 그림은 Log Likelihood의 수식을 나타낸 그림입니다. 마지막 항이 Jacobian의 Determinant로 표현되는데요. 이를 구할 수 있어야 최종적으로 x의 확률 분포를 계산할 수 있습니다. 따라서 딥러닝 모델을 구성하면서 함수를 선택할때 Jacobian의 Determinant를 쉽게 계산할 수 있는지도 따져봐야 합니다.

4-2. NICE

이러한 어려움으로 인해 비교적 간단한 이론임에도 불구하고 딥러닝 모델로 구현한 Normalizing Flow가 없었는데요. 2015년 최초로 NICE라는 모델이 딥러닝을 사용하여 Normalizing Flow를 구현합니다.

NICE의 핵심 아이디어는 함수 f를 Coupling Layer를 사용하여 구성하는 것입니다. Coupling Layer란 구성 값을 반반으로 나누어 구성해주는 방법입니다. 예를 들면 이렇게 되는거죠.

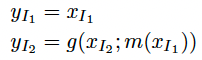
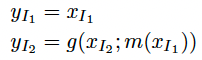
이어서 g를 Additive (+)로 표현해주면 수식은 이렇게 되는데요.

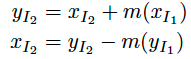
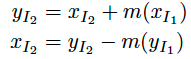
이렇게 구성해주면 Jacobian의 Determinant를 쉽게 구할 수 있습니다. 먼저 Jacobian은 이렇게 나오죠.

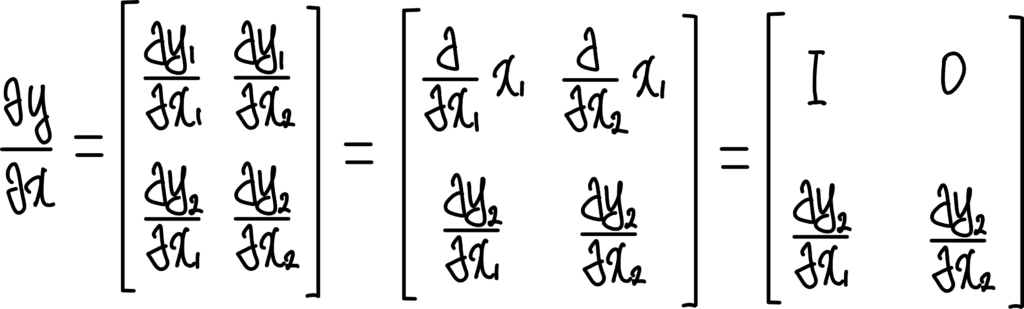
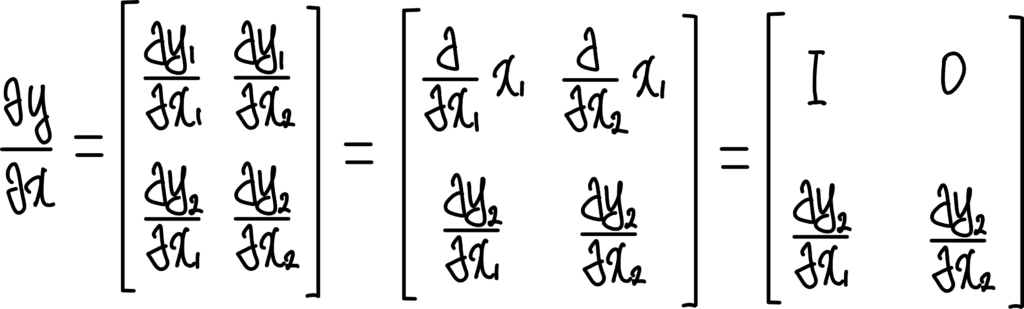
따라서 Jacobian의 Determinant는 이렇게 됩니다.

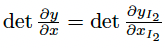
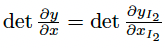
그리고 y2를 대입하면 최종적으로 수식은 이렇게 정리됩니다.

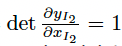
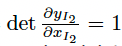
그럼 f의 역함수도 구할 수 있는지를 확인 해봐야겠죠? 함수 f의 역함수는 이렇게 간단하게 구할 수 있습니다.

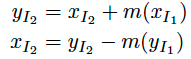
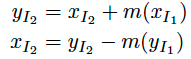
이렇게 구현한 NICE가 생성한 이미지는 이렇습니다.

제법 그럴듯한 이미지들을 생성하는 모습이죠?

4-3. RealNVP

다음은 2017년도에 ICLR에 발표된 RealNVP 모델을 살펴보겠습니다. NICE에서는 내부 함수 g를 단순한 Additive 함수를 적용했는데요. 이로 인해 복잡한 데이터 분포는 표현하기 어렵다는 한계가 있었습니다. 이러한 한계를 극복하기 위해 RealNVP에서는 내부 함수 g를 Affien Transformation으로 구성해줍니다. 수식으로는 이렇게 표현됩니다.

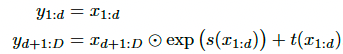
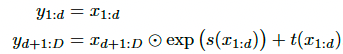
이렇게 Affine Transformation으로 표현해줘도 Jacobian의 Determinant는 쉽게 구할 수 있습니다. 먼저 Jacobian은 이렇게 표현되고요.

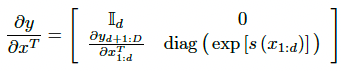
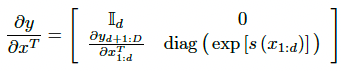
이에 대한 Determinant는 이렇게 깔끔하게 나옵니다.

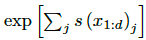
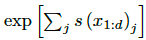
뿐만 아니라 역함수도 이렇게 쉽게 구할 수 있죠.

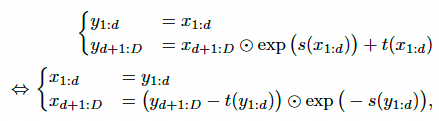
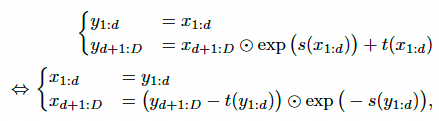
이렇게 구성된 RealNVP가 생성한 이미지들은 이렇습니다.

확실히 NICE보다 훨씬 고화질이고 정교하게 표현하는 모습이죠?

4-4. Glow

마지막으로 2018년 NIPS에 발표된 Glow를 살펴보겠습니다. Glow의 포인트는 세가지 입니다.

첫 번째는 Actnorm입니다. 이는 Batch Normalization과 유사한 역할을 합니다.
두 번째는 Invertible 1×1 Convolution입니다. 이는 Coupling Layer의 구성 조합을 다양하게 만들어주는 역할을 합니다.
세 번째는 Affine Coupling Layer입니다. 이는 RealNVP와 동일한 방법이죠.

이렇게 구성된 Glow가 생성한 이미지들은 이렇습니다.

기존 NICE, RealNVP보다 훨씬 고화질이고 선명하면서 정교한 이미지를 생성하는 모습을 볼 수 있습니다.

출처

1. Dinh, Laurent, Jascha Sohl-Dickstein, and Samy Bengio. “Density estimation using real nvp.” arXiv preprint arXiv:1605.08803 (2016).